Um desafio central para a criação de computação quântica praticamente valiosa é a supressão de erros. Hoje, o custo desta supressão parece proibitivo. Para cada qubit lógico incluído no algoritmo, devem ser usados até 1.000 qubits físicos. Recentemente, um grupo de cientistas dos Estados Unidos mostrou que os custos indiretos podem ser reduzidos significativamente, o que promete amplas perspectivas para a computação quântica.

Fonte da imagem: geração AI Kandinsky 3.0/avalanche noticias
Uma equipe de Harvard liderada pelo ex-professor graduado do MIPT Mikhail Lukin, um dos principais cientistas do mundo em sistemas quânticos, demonstrou a operação de algoritmos quânticos livres de erros em 48 qubits lógicos em uma matriz de 280 qubits físicos. Usando controle de nível lógico e arquitetura zoneada em matrizes reconfiguráveis de átomos neutros, o sistema combina portas de dois qubit de alta confiabilidade, conectividade arbitrária e rotações de um qubit totalmente programáveis.
O computador quântico criado pelo grupo de Lukin no laboratório de Harvard explora defeitos em estruturas cristalinas. Podem ser diamantes artificiais, onde são colocados átomos de rubídio super-resfriados. A programação de tais sistemas é realizada com pinças laser. Primeiro, os átomos são preenchidos aleatoriamente em defeitos e, em seguida, a matriz é “programada” movendo os átomos para os defeitos incluídos no circuito para executar o algoritmo (simulação).
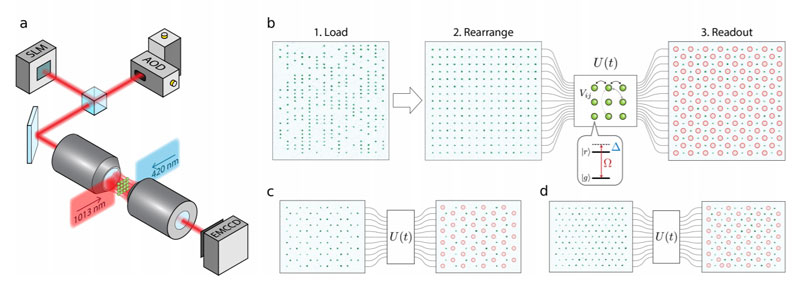
Esquema para obtenção de matrizes bidimensionais a partir de átomos neutros e formação de estruturas com diferentes arranjos de átomos excitados. Fonte da imagem: Natureza
Usando uma série de algoritmos de complexidade variada, o grupo de Lukin mostrou que o uso superredundante de qubits físicos para cada qubit lógico é, em geral, desnecessário. Para que os cálculos ocorram com precisão satisfatória, até 7 qubits físicos por lógico podem ser suficientes, conforme descrito em trabalho publicado em 6 de dezembro na revista Nature.
Esses resultados sugerem a chegada da computação quântica com correção de erros, mais cedo ou mais tarde. Isto abrirá aplicações e impulsionará uma mudança na abordagem dos desafios e oportunidades na computação quântica.