Nem todos os que vagueiam estão perdidos
J. R. R. Tolkien
A pesquisa no espaço de estados é um grupo de métodos matemáticos projetados para resolver problemas de inteligência artificial.
Wikipedia
⇡#Pesquisa no espaço de estado: da declaração do problema à solução
Vamos começar com a prática e tentar resolver o problema clássico de IA. Assim, três missionários e três canibais estão na mesma margem do rio, onde também há um barco que pode acomodar no máximo duas pessoas. Encontre uma maneira de transportar todos para o outro lado do rio, deixando os missionários em lugar nenhum menos do que canibais. Esse problema foi amplamente discutido em uma época e foi analisado em detalhes em 1968 por Amarel. Na década de 1960, os algoritmos de pesquisa despertaram um grande interesse e as estratégias para resolvê-los tornaram-se parte da problemática clássica da IA. No final do artigo, mostraremos uma árvore para resolver este problema e agora analisaremos alguns termos importantes.
Qualquer algoritmo de pesquisa pega algum problema como entrada e retorna uma solução na forma de uma sequência de ações. Para começar, vamos descobrir em que elementos consistem os conceitos “objetivo”, “tarefa” e sua “solução”. Então, vamos imaginar que estamos descansando em um resort onde nos deparamos com uma tarefa complexa e multifacetada – fazer da melhor maneira possível passar nossas tão esperadas férias. Para a sua implementação, é necessário levar em consideração muitos fatores: se você gosta de vida noturna, você precisa escolher uma zona turística movimentada; se você quer apenas passear pela cidade, tem que visitar os parques, as ruas mais pitorescas, etc. Ótimo, você está descansando, a lista de afazeres está longe de estar completa, mas … você tem uma passagem para Moscou por amanhã isso não pode ser devolvido. Você vai voar, mesmo que ainda não tenha estado em todos os lugares e não tenha provado todas as iguarias locais?
Então, neste caso, você é um agente de decisão. No seu caso, você precisa se esforçar para atingir o objetivo – entrar no avião. Todas as outras ações irão apenas atrapalhar você. O primeiro passo é formular uma meta com base em sua situação atual e seu desempenho como agente de tomada de decisão. O estabelecimento de metas permite organizar o comportamento, limitando o agente na escolha de estágios intermediários. Acredito que todos têm uma compreensão intuitiva do objetivo e estamos familiarizados com a necessidade de sacrificar algo para alcançá-lo. Assim, a tarefa do agente de tomada de decisão é encontrar a sequência de ações que o levará ao estado de destino. Essa sequência é chamada de pesquisa.
Ótimo, há um objetivo, uma tarefa – como chegar lá e o que vem a seguir? Além disso – a formulação da tarefa, uma etapa muito importante para a realização bem-sucedida de seu objetivo. Ou seja, você provavelmente tentará descobrir como chegar ao aeroporto, quanto tempo leva para chegar até ele, – quais ações e estados você precisa levar em consideração para atingir seu objetivo. Falando formalmente, o problema consiste em quatro partes: um estado inicial, um conjunto de ações, uma função de verificação de meta e uma função de custo do caminho. As duas últimas definições provavelmente precisam ser explicadas.
Função de verificação de metas: cheguei ao meu destino? Função de custo do caminho: quanto me custa cada etapa? No caso mais trivial, o custo de uma sequência de ações é igual ao número das próprias ações. Na verdade, é claro, cada etapa é desigual e tem seu próprio custo. Agora, por que estamos falando sobre busca no espaço de estados: o ambiente do problema é representado pelo espaço de estados, e o caminho através dele do estado inicial para o estado de destino é uma solução. Algoritmicamente, vamos dizer o seguinte: para resolver o problema, usaremos a pesquisa baseada em árvore, e suas várias variações incorporam várias estratégias possíveis.
⇡#Pesquisa desinformada
Normalmente, são estudadas cinco estratégias de busca não informada – aquela em que nenhuma outra informação sobre os estados é utilizada, exceto aquela na condição problema. Essas estratégias só podem desenvolver sucessores e distinguir entre os estados alvo e não alvo. No entanto, eles são a base de muitos dos métodos atuais. Todas as estratégias de pesquisa diferem na ordem em que os nós são expandidos. Listaremos essas estratégias abaixo para sua informação e detalharemos as duas principais:
- Largura da primeira pesquisa,
- Pesquisar por critério de custo,
- Pesquisa em profundidade,
- Pesquisa com profundidade limitada,
- Pesquisa em profundidade com aprofundamento iterativo,
- Pesquisa bidirecional.
A tarefa com a qual começamos a história de hoje é resolvida usando uma pesquisa em largura (BFS). Este é um dos métodos clássicos de percorrer um grafo, no qual visitamos ao mesmo tempo os vizinhos mais próximos de nosso ponto de partida, depois seus “vizinhos”, enquanto calculamos a distância (número mínimo de arestas) de nosso ponto de partida a cada vértice acessível a partir dele. Assim, avançamos em largura até encontrar o ponto desejado ou até que a fila de vizinhos termine. Por algum motivo, a imagem da captura de um criminoso me vem à mente, quando são realizadas buscas simultaneamente em vários setores da cidade ao redor da cena do crime, proporcionando a cobertura mais completa do território. Vamos escrever este algoritmo em Python:
S [começar] = 0
Q = [começar]
Qbegin = 0
Enquanto Qbegin u = Q [Qbegin]
Qbegin + = 1
Para v em V [u]:
Se S [v] for Nenhum:
S [v] = S [u] + 1
Agora, vamos dar uma olhada na pesquisa em profundidade. Ao pesquisar em profundidade, apenas os nós que estão no caminho da raiz ao nó atual são armazenados na memória. Simplificando, do ponto de partida damos um passo, dele outro e assim avançamos até atingir o estado de destino ou para um estado do qual é impossível ir mais longe. Se isso acontecer, o algoritmo retorna recursivamente e avança do ponto de retorno até que uma solução seja encontrada. Se você já se perdeu em algum momento, imagine o princípio desse algoritmo: o telefone descarrega, você entende que está indo para o lugar errado, volte a um monumento conhecido e procure um caminho para sair dele em uma direção diferente. Esta é a aparência de uma implementação Python:
Caminho = [Nenhum] * (n + 1)
Def dfs (iniciar, visitado, caminho, g):
Visitado [começar] = Verdadeiro
Para u em g [início]: # variável u visita todos os vizinhos do vértice início
Se não for visitado [u]:
Caminho [u] = começo
Dfs (u)
Considere novamente um gráfico com vértices de 1 a n. Vamos iniciar o algoritmo dfs (acrônimo em profundidade primeira pesquisa): chamamos o vértice de begin, os nós que podem ser alcançados a partir dele serão incluídos na lista visitada (em linguagem formal, vértices que estão no mesmo componente conectado com begin). Do topo, vamos olhar para todos os nós vizinhos e visitar cada um. Ao visitar vizinhos, vamos olhar para seus vizinhos. Precisamos da lista de caminhos para construir caminhos do início até todos os vértices disponíveis. Como você pode ver, esse algoritmo é baseado na recursão. Para evitar que ele entre em loop, precisamos marcar quais vértices visitamos anteriormente (na lista visitada). E os predecessores de cada vértice são armazenados para que mais tarde você possa construir uma árvore de busca.
Acima, existem duas estratégias principais para pesquisa desinformada. Se quiser saber mais, recomendamos a leitura do livro “Artificial Intelligence: A Modern Approach” (Stuart Russell, Peter Norvig).
Pesquisa informada
Geralmente, as estratégias de pesquisa informadas são consideradas mais eficazes para encontrar uma solução. O princípio geral aqui é Best-First-Search. Existe toda uma família de algoritmos desse tipo com diferentes funções de estimativa. Uma característica distintiva desses algoritmos é uma função heurística denotada como h (n): h (n) = estimar o custo do caminho menos caro do nó n ao nó de destino. Como exemplos, consideraremos brevemente a chamada busca gananciosa e em mais detalhes – o algoritmo A *.
Pesquisa A *: Minimize a estimativa de custo total da solução. A * search é o algoritmo de busca de melhor correspondência mais famoso. A razão de seu sucesso está na função de avaliação – o algoritmo toma a decisão mais racional em cada etapa. É mais conveniente descrevê-lo formalmente:
F (n) = estimar o custo do caminho de solução menos caro através do nó n.
F (n) = g (n) + h (n), onde g (n) é o custo de se chegar a este nó e h (n) é o custo de viajar deste nó ao destino. Para encontrar a solução menos dispendiosa, é melhor escolher o nó com o valor mais baixo para esta função. Como se viu, a busca por A *, sujeita a certos requisitos para suas heurísticas (e quais responderemos no próximo artigo), pode ser completa e ótima, então essa estratégia é totalmente justificada. Foi interessante para você escrever um programa para A * ou é muito código? Por enquanto, vamos resolver um pequeno problema com seu aplicativo:
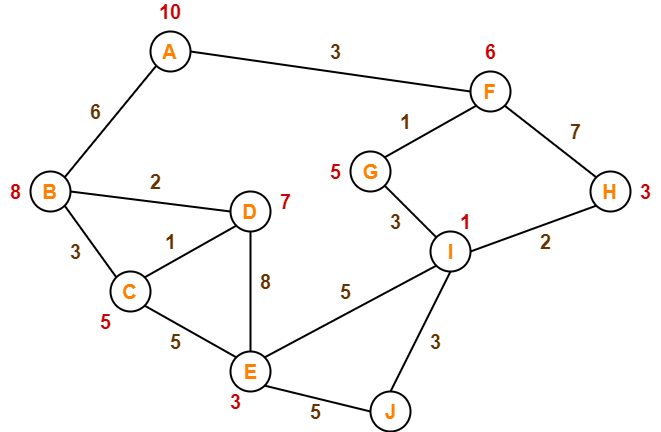
Considere este gráfico. Como A * vai contornar isso?
- Começamos do nó A.
- Do nó A, você pode chegar ao nó B e ao nó F.
O algoritmo A * calculará f (B) e f (F).
- F (B) = 6 + 8 = 14
- F (F) = 3 + 6 = 9
Caminho: A → F
Do nó F você pode chegar ao nó G e ao nó H.
O algoritmo A * calculará f (G) e f (H).
- F (G) = (3 + 1) + 5 = 9
- F (H) = (3 + 7) + 3 = 13
Caminho: A → F → G
Etapa 3:
Do nó G só se pode chegar ao nó I.
O algoritmo A *, no entanto, calculará f (I).
- F (I) = (3 + 1 + 3) + 1 = 8
A decisão foi tomada para ir para o nó I.
Caminho: A → F → G → I
Do nó I, você pode chegar ao nó E, H e J.
O algoritmo A * calculará f (E), f (H) e f (J).
- F (E) = (3 + 1 + 3 + 5) + 3 = 15
- F (H) = (3 + 1 + 3 + 2) + 3 = 12
- F (J) = (3 + 1 + 3 + 3) + 0 = 10
Como o valor de f (J) é menor, decidiu-se ir para o nó J.
Caminho: A → F → G → I → J
A história sobre algoritmos de busca não pode ser completa sem um algoritmo genético, mas um artigo separado precisará ser dedicado a ela. O curso de IA da universidade também explora a contra-pesquisa usando minimax search e alpha-beta clipping – mais sobre isso em outro momento. E agora a árvore prometida para o problema desde o início do artigo.
Observe que descartamos a situação em que há apenas uma pessoa no barco, porque a segunda pessoa deve levá-la de volta. Então, apenas dois canibais ou um missionário com um canibal podem nadar juntos. Isso é mostrado nos dois únicos nós possíveis que emanam do vértice. Também é possível que o barco saia e volte com os mesmos personagens, isso não é mostrado no diagrama. No entanto, se você compor um algoritmo, deverá levar essa situação em consideração. Além disso, o problema é resolvido sem problemas, uma vez que foram alcançados os estados, a partir dos quais a travessia pode ser realizada de acordo com as condições do problema.

Esperamos que nossa história sobre algoritmos de pesquisa em IA tenha feito você querer entendê-los mais profundamente e, possivelmente, tentar escrever seus próprios programas.
Fontes:
- Stuart Russell, Peter Norvig. Inteligência Artificial: Uma Abordagem Moderna.
- Material didático do curso “Inteligência Artificial e Suas Aplicações Industriais” do Instituto Nacional de Ciência e Tecnologia de Taiwan.
