No final de 2025, o presidente dos EUA, Donald Trump, expressou sua intenção de fornecer financiamento federal parcial para empresas de computação quântica, semelhante à decisão do governo de se tornar acionista minoritário da Intel em meados daquele ano. Essas empresas incluem IonQ, Rigetti Computing, D-Wave Quantum, Quantum Computing e Atom Computing, entre outras, que fizeram progressos significativos nessa área. Os representantes dessas empresas, em geral, receberam a notícia com entusiasmo: qualquer pesquisa promissora na indústria de TI exige investimentos substanciais com um período de retorno incerto, e a criação de computadores quânticos reais é ainda mais complexa. Além disso, não basta simplesmente aprender a criar e entrelaçar um número significativo de qubits por um longo período: também é necessário corrigir efetivamente os erros que inevitavelmente se acumulam durante a operação desses sistemas. Recentemente, exploramos uma abordagem para a correção eficaz de erros em computação quântica, a verificação de paridade de baixa densidade da IBM; agora é hora de examinar os métodos usados por outros pesquisadores.

Representação artística inspirada de uma porta lógica de emaranhamento quântico (fonte: Universidade de Sydney)
⇡#RosettaDisturbs
No final do século XVIII, um artefato foi descoberto no Egito, fornecendo a chave para decifrar a escrita hieroglífica: a Pedra de Roseta, contendo o mesmo texto escrito três vezes: em hieróglifos egípcios antigos, na escrita demótica posterior e em grego antigo. Desde então, o termo “Pedra de Roseta” tem sido usado na ciência e na tecnologia para descrever descobertas que, por meio de uma analogia bem-sucedida, nos permitem compreender — e, tendo compreendido o que compreendemos, reproduzir — algo antes inacessível. A porta lógica quântica, demonstrada em agosto de 2025 por pesquisadores do Laboratório de Controle Quântico do Instituto de Nanotecnologia da Universidade de Sydney, foi apelidada de “Pedra de Roseta da computação quântica” porque permite (pelo menos em teoria) uma redução radical no número de qubits físicos necessários para criar uma única porta lógica. Para relembrar, em 2026, a IBM planeja lançar um computador quântico de 12 qubits, construído com 288 qubits físicos e capaz de realizar cálculos com um erro de no máximo 0,1%. Isso significa que cada qubit lógico exigirá 24 qubits físicos, organizados em um circuito de correção de erros altamente complexo. E isso é apresentado, com razão, como uma conquista significativa: se um computador similar for criado com base em um algoritmo de correção de erros superficial (usado, por exemplo, pelo Google em sua série de computadores quânticos Willow), então, para formar a mesma dúzia de qubits lógicos e alcançar esse resultado, seriam necessários 24 qubits físicos.Para um circuito computacional com erro computacional semelhante, seriam necessárias quase 3.000 portas lógicas físicas — uma ordem de magnitude a mais.
Um circuito de computação quântica, similar a um circuito clássico, consiste em um certo número de portas lógicas conectadas em uma ordem específica; a passagem de sinais por esse circuito realiza o cálculo. Uma porta lógica, abstraindo-se de sua implementação física, pode ser considerada um operador que, de acordo com regras estabelecidas, transforma o(s) sinal(is) de entrada em sinal(is) de saída (é importante enfatizar que o número de entradas e saídas para portas quânticas deve ser igual devido à exigência de unitariedade). No caso da computação quântica, os sinais são os estados de qubits específicos que participam do cálculo. Contudo, ao longo de todo o cálculo, os qubits devem permanecer objetos quânticos, ou seja, manter um estado de superposição, sem colapsar para nenhum dos estados limites — |0⟩ ou |1⟩. Portanto, portas quânticas que envolvem operações com dois ou mais qubits devem emaranhar esses mesmos qubits (portas lógicas de emaranhamento) — isto é, formar correlações quânticas entre seus operandos, de modo que medir o estado de um dos qubits emaranhados determine instantaneamente e sem ambiguidade o estado do outro. Um exemplo básico de uma porta de emaranhamento é a NOT controlada (CNOT): seus operandos são dois qubits — o alvo e o controle. Se o controle colapsar para o estado |1⟩, então o alvo deve assumir imediatamente um estado inverso ao seu estado original, qualquer que seja ele. Lembremos mais uma vez que todas as operações dentro de um circuito de computação quântica, enquanto ele permanece no estado |1⟩, são realizadas em um circuito de computação quântica.As superposições são completamente reversíveis e, portanto, não é totalmente correto dizer que o CNOT “muda o estado do qubit alvo para o oposto”: no final, ele o mudará, sim, mas até que a incerteza quântica seja resolvida, todas as possibilidades que estão em princípio disponíveis permanecem ocultas no estado de superposição de um sistema quântico emaranhado.

Uma ilustração do artigo da Nature Physics em discussão, mostrando a implementação de uma porta quântica de um único qubit (a) e de dois qubits (b) usando um íon de itérbio aprisionado (c), bem como um esquema para conduzir medições de modo único e duplo usando o protocolo GKP (d) (Fonte: Universidade de Sydney).
A essência da porta quântica de emaranhamento proposta pelos pesquisadores de Sydney é que ela implementa o código Gottesman-Kitaev-Preskill (GKP), nomeado em homenagem a Daniel Gottesman, Alexey Kitaev e John Preskill, que publicaram o trabalho correspondente em 2001. Comparar o GKP à Pedra de Roseta faz sentido porque esse protocolo cria uma representação exata de qubits — ou mais precisamente, de quaisquer sistemas quânticos cuja dimensão do espaço de Hilbert seja finita — em outro sistema quântico, representado, por exemplo, por osciladores; ele traduz, figurativamente falando, a escrita hieroglífica egípcia antiga para o grego clássico sem distorcer a mensagem codificada na primeira. O protocolo é baseado nos chamados estados de rede, invariantes em relação a um deslocamento de valor fixo: essa “rede” repetitiva permite detectar e corrigir facilmente pequenos erros no deslocamento dos estados dos qubits. Acontece que um estado de rede construído corretamente — isto é, um operador de deslocamento escolhido corretamente para gerá-lo — substitui toda uma série de qubits de controle, que teriam que ser emaranhados com o original para o controle contínuo de seu estado. No entanto, neste caso, evita-se a redundância física no número de qubits necessários (paraA implementação de uma única sequência lógica é alcançada através da construção de um sistema bastante complexo, que, em princípio, é capaz de armazenar informações sobre as oscilações (estados vibracionais) dos qubits, utilizando códigos bosônicos. Em outras palavras, nem todo sistema quântico pode ser corrigido usando o GKP, e este protocolo não é capaz de corrigir todos os erros, apenas os relativamente pequenos.
Um grupo de pesquisadores de Sydney colocou um íon de itérbio isolado, cujo estado de energia é caracterizado por um espectro de oscilação natural, em uma armadilha de Paul. Este espectro, por sua vez, surge da interação do campo eletromagnético da partícula com um campo externo que a confina em uma região específica do espaço. Este espectro é discreto, o que permite codificar primeiro um qubit no oscilador harmônico resultante usando o protocolo GKP, e depois o segundo: como o íon aprisionado oscila em três dimensões, seu deslocamento em cada uma delas pode ser considerado um estado quântico separado, e como o íon é o mesmo, as oscilações em duas dimensões são naturalmente emaranhadas. Em mecânica quântica, osciladores harmônicos e bósons (partículas que obedecem à estatística de Bose-Einstein) são descritos por operadores semelhantes e, portanto, tais esquemas de processamento de informação quântica — que utilizam espaços de Hilbert de dimensão infinita de osciladores harmônicos para codificar qubits lógicos com capacidade de correção de erros — são chamados de bosônicos. Além das oscilações mecânicas de íons aprisionados, queUm grupo de Sydney argumentou que circuitos bosônicos podem ser implementados, em particular, usando modos eletromagnéticos em ressonadores de micro-ondas e fótons ópticos. No entanto, uma característica específica dessa abordagem, ou seja, o uso de osciladores harmônicos, complica a criação de um conjunto universal de portas lógicas para operações quânticas dentro do protocolo GKP. Portanto, mesmo que a configuração laboratorial proposta pelos pesquisadores evolua com o tempo para um computador quântico funcional, o leque de problemas que podem ser resolvidos por ele será ainda mais restrito do que o abrangido pelos algoritmos quânticos. Contudo, uma vantagem significativa da abordagem proposta pelos pesquisadores é a dispensa do resfriamento criogênico: o íon de itérbio é confinado dentro de uma armadilha de Paul por lasers à temperatura ambiente.

A armadilha de Paul em si é um conjunto de eletrodos colocados dentro da câmara de vácuo mostrada aqui. Se estas forem as dimensões de uma única porta de um computador quântico promissor (um que não exija qubits de correção adicionais), um projeto prático — com talvez mil qubits lógicos — seria verdadeiramente monstruoso (fonte: Wikimedia Commons).
⇡#É pura mágica!
Os fenômenos quânticos são fundamentalmente diferentes dos fenômenos macroscópicos que percebemos diretamente: basta mencionar a não-localidade do emaranhamento quântico, ou seja, o colapso instantâneo (não limitado pela velocidade da luz, a velocidade limite do nosso Universo, mas sim instantâneo) do estado de um dos objetos quânticos previamente emaranhados, exatamente quando o estado do outro é medido, independentemente da distância entre eles. É por isso que emular computadores quânticos em computadores clássicos não é apenas difícil, mas — além de um certo nível de complexidade — não confiável: é simplesmente impossível programar algoritmicamente e exaustivamente manifestações fisicamente corretas de efeitos quânticos em sistemas verdadeiramente complexos. Agora está claro por que, ao descrever os computadores quânticos mais promissores, os pesquisadores falam em estados mágicos. Trata-se de configurações especiais de sistemas quânticos que não podem ser reproduzidas por meios clássicos, por mais que se tente — e é precisamente graças a essas configurações que a superioridade quântica sobre sistemas arbitrariamente complexos será (como esperado) alcançada um dia.Computadores semicondutores.
A porta CNOT mencionada anteriormente, descrita em detalhes no artigo anterior sobre correção de erros quânticos (código de superfície), e diversas outras operações amplamente utilizadas hoje por desenvolvedores de computadores quânticos são as chamadas portas de Clifford. Por um lado, elas são bastante eficazes para realizar importantes operações de computação quântica (emaranhamento de qubits, correção de erros, etc.), mas, por outro, não são tão quânticas assim quando analisadas mais de perto. Mais precisamente, essas portas simplificam as interações de objetos quânticos de forma tão eficaz — privando-os da aura mágica de estranheza e da falta de analogias diretas com fenômenos macroscópicos — que as operações que as envolvem são perfeitamente emuladas pelos computadores clássicos mais comuns. Sim, com um gasto monstruoso de tempo, energia e recursos de hardware; mas a superioridade quântica dos circuitos de Clifford sobre os computadores semicondutores convencionais é puramente quantitativa, e nem sequer a maior. Formalmente, não há trapaça: os computadores de Clifford de hardware realmente realizam operações quânticas em qubits reais e produzem resultados muito mais rapidamente do que se o mesmo problema fosse resolvido em um computador clássico. No entanto, o teorema fundamental de Gottesman-Knill afirma que qualquer computação quântica composta por operações de Clifford também pode ser realizada em um computador clássico — em tempo polinomial. Em outras palavras, confiar exclusivamente em portas de Clifford permite obter apenas um computador quântico irreversível — emEm certo sentido, é análogo ao computador clássico, para o qual a flecha do tempo é rigidamente definida; ela é definida pelo próprio fato de que os cálculos, como assumem seus criadores, podem gerar erros, os quais, por sua vez, podem ser corrigidos, essencialmente retornando o sistema a um estado anterior para recálculo. Mas, no nível quântico, os processos são completamente simétricos em relação à escolha da direção em que o tempo flui; portanto, um computador quântico universal, como já enfatizamos repetidamente, deve ser completamente reversível — até que um determinado resultado seja obtido, ou seja, até que a função de onda colapse.

Uma representação geométrica do código quântico de Reed-Muller, que usa 15 qubits físicos para formar um único código lógico com distância-3 (ou simplesmente d3, o que significa que ele pode detectar e corrigir um erro). Este é o menor código d3 em termos do número de componentes que permite a criação de uma porta T não-Clifford, e é usado com mais frequência do que outros esquemas para destilar estados mágicos (fonte: arxiv.org/abs/2507.12511).
Qual o problema com as portas Clifford? Afinal, se uma emulação semicondutora de um computador quântico baseada nelas leva décadas para resolver um problema, enquanto um computador de hardware com 1000 qubits o resolve em alguns meses (em vez de alguns minutos, como seria o caso se proporcionasse um ganho de tempo exponencial em vez de polinomial), qual a diferença se é universal ou não? Para aqueles cuja área de interesse é diretamente afetada pelo problema resolvido (para criptógrafos, por exemplo, que terão que abandonar a criptografia RSA de qualquer forma), a diferença é de fato pequena. Mas a gama de algoritmos executados com sucesso em computadores Clifford não é tão extensa — e, mais importante, alcançar ganhos de tempo exponenciais onde eles ainda não existem é muito desejável. Só para garantir, vamos refrescar nossa memória sobre o significado de um computador quântico universal de múltiplos qubits: se o número de qubits em um estado de superposição nele é L, então o número total de estados linearmente independentes de tal sistema é 2L. E todo o processo de computação em tal computador se resume essencialmente a uma única rotação do vetor de estado em um espaço de Hilbert de dimensão 2L. E para implementar tal rotação, é muito necessárioOperar livremente sobre os estados de qubits emaranhados. Enquanto a porta S (porta de fase), que rotaciona o vetor de estado de um único qubit em uma esfera de Blochan em 90° em relação ao eixo Z, é uma porta de Clifford, a porta T, que também rotaciona, mas apenas em 45°, não é. Encontrar uma implementação física da porta T é perfeitamente possível, mas aqui está o problema: implementar um sistema de correção de erros tão confiável (embora complexo) quanto o aplicável às portas de Clifford não será mais possível. Não é o mesmo sistema!
Há mais de duas décadas, Emanuel Knill, coautor do teorema de Gottesman-Knill e um dos pilares de toda a teoria moderna da computação quântica, propôs a ideia de computação quântica com filtragem pós-seletiva. A proposta era encontrar um circuito de filtragem desse tipo — quântico, é claro; integrado organicamente em um computador quântico, que aceitaria dados de saída (incluindo aqueles provenientes de portas ruidosas) para processamento posterior somente se os resultados da medição satisfizessem condições predeterminadas. O circuito de filtragem seria composto por qubits auxiliares, pré-configurados para um estado mágico, de forma que, ao transmitirem esse estado para uma porta de Clifford, o resultado seja exatamente o mesmo que se a entrada fosse o resultado de uma operação não-Clifford (a mesma rotação T, por exemplo). Como resultado, todo o sistema volta a ser Clifford (embora Knill não tenha especificado exatamente como implementar qubits lógicos mágicos funcionais), e os algoritmos voltam a ser aplicáveis a ele.correção de erros — mas agora sua vantagem de velocidade em relação a um computador de von Neumann está significativamente mais próxima de uma função exponencial do que polinomial. Mais próxima, porque a necessidade de corrigir os erros detectados ainda torna os cálculos mais lentos — mas ainda assim é uma melhoria significativa.

Um dispositivo para destilar estados mágicos — baseado no Gemini, um computador quântico que usa átomos neutros como qubits (fonte: QuEra)
⇡#PrazerCaro
Estados mágicos, ou estados mágicos, são, portanto, estados quânticos pré-preparados que são então usados como recursos (catalisadores, em termos gerais) por algoritmos quânticos mais complexos, quase universais, para executá-los em sistemas de Clifford. O processo de preparação desses estados é chamado de destilação (destilação de estados mágicos). Em meados de 2025, a QuEra Computing, com sede em Boston, Massachusetts, demonstrou a destilação de estados mágicos em qubits lógicos — demonstrando, de forma importante, a viabilidade fundamental do objetivo de Knill: um salto qualitativo de ganhos de tempo polinomiais para exponenciais usando computadores quânticos. É importante notar que o próprio procedimento de destilação já havia sido implementado significativamente antes em qubits físicos; A conquista da QuEra, no entanto, foi adaptá-la especificamente para qubits lógicos, representados por um grupo inteiro de qubits físicos mutuamente emaranhados. A taxa de erro típica na computação quântica até então era, na melhor das hipóteses, de 10⁻³: um erro a cada mil operações. O uso da destilação de estado mágico, segundo os pesquisadores, possibilitou melhorar imediatamente esse resultado para 10⁻⁹. E embora a diferença em relação aos valores típicos para computadores semicondutores ainda seja enorme, de 8 a 10 ordens decimais, o notório computador quântico…A superioridade do literal momentaneamente adquiriu contornos significativamente mais realistas.
Como, então, a “magia” dos estados mágicos se realiza? Os físicos não mencionam “magia” aqui por mero capricho: os fenômenos quânticos são verdadeiramente tão incomuns da perspectiva de nossa experiência macroscópica que se encaixam perfeitamente na definição do milagroso, extraída dos contos de fadas. Provavelmente todos se lembram da escola da influência de um observador (em sentido amplo, como um dispositivo que registra estados quânticos; não necessariamente um ser vivo e inteligente) sobre os processos quânticos: uma partícula elementar se comporta como uma onda ou um corpúsculo, dependendo de qual de suas propriedades está sendo registrada em um dado momento. O princípio da incerteza de Heisenberg também é bem conhecido: é impossível medir simultaneamente com precisão certos parâmetros relacionados de um objeto quântico — suas coordenadas e momento, sua corrente e voltagem, e as intensidades de seus campos elétrico e magnético. No entanto, a questão não para por aí: verifica-se que as medições de várias propriedades dos próprios objetos quânticos não podem ser vistas simplesmente como fixações independentes de valores objetivamente existentes e inequívocos. Grosso modo, a primeira medição já altera o estado do sistema quântico e, portanto, o valor da segunda (mesmo que uma característica completamente diferente seja medida) dependerá inevitavelmente do resultado obtido com a primeira — isso é chamado de contextualidade quântica. O resultado da medição de uma dada grandeza no mundo quântico depende da escolha de outras grandezas medidas simultaneamente com ela — formando, assim, um contexto.medidas.
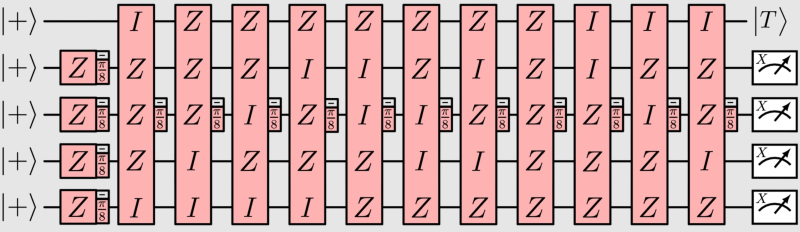
Um possível protocolo de destilação usando 5 qubits lógicos. Cada porta corresponde a uma rotação de um ou mais qubits, que pode ser implementada usando um único estado inicial |T⟩. Após 15 rotações desse tipo, os valores dos quatro estabilizadores do tipo X do código de Reed-Muller são calculados a partir das medições dos qubits lógicos 2 a 5 na base X. Se todos os resultados das medições forem +1, a destilação é bem-sucedida e o primeiro qubit lógico está no estado |T⟩ (fonte: arxiv.org/abs/2507.12511).
A contextualidade quântica é uma propriedade bastante mágica para os nossos padrões (clássicos); trata-se de uma espécie de correlação não clássica de grandezas físicas independentes (aparentemente, de acordo com a nossa lógica usual). Os estados mágicos estão diretamente relacionados a ela: existem objetivamente (já que podem ser registrados por dispositivos), mas não são descritos por modelos clássicos — e precisamente por essa razão, as portas de Clifford não se aplicam a eles. Levar em consideração o “distanciamento” de um estado mágico em relação ao que pode ser reproduzido por meios clássicos — muitos pesquisadores ironicamente chamam a medida desse distanciamento de “mana quântica” — é precisamente o que permite à computação quântica se libertar das amarras da imitação clássica, impostas pela necessidade de usar exclusivamente calculadoras de Clifford para corrigir os erros inevitáveis. Essa inevitabilidade é determinada de forma bastante objetiva: os limites do mundo quântico são extremamente estreitos (ligados aos tamanhos característicos de partículas elementares individuais, em casos extremos, átomos e moléculas), enquanto os computadores quânticossão inevitavelmente macroscópicos. É precisamente a discrepância entre a escala dos sistemas que realizam computações quânticas e a dos seus elementos, aos quais as leis do mundo quântico são plenamente aplicáveis, que dá origem aos sérios problemas técnicos que os pesquisadores precisam superar com tanto esforço.
Em resumo: estados mágicos, embora “mágicos” em sua natureza quântica, não surgem com a onda de alguma nanopartícula: eles são formados dentro do próprio computador quântico, usando meios semelhantes aos que os engenheiros utilizam para construir circuitos quânticos convencionais. Em um nível qualitativo, tudo é bastante transparente: qualquer qubit físico individual será inevitavelmente ruidoso. No entanto, se um número suficiente de cópias for criado, o procedimento de destilação, descrito inicialmente em um rascunho por Emanuel Knill e posteriormente detalhado no trabalho de Sergey Bravyi e Alexei Kitaev, permitirá, reduzindo drasticamente seu número, produzir um pequeno lote de qubits que são virtualmente “puros”, livres de ruído parasita. Trata-se essencialmente de correção de erros, mas no nível dos estados, não das operações. Além disso, a destilação repetida (embora com um aumento exponencial no número de cópias originais — outro processo que consome muitos recursos!) torna possível reduzir a taxa de erro do estado mágico a um nível arbitrariamente baixo. E isso é uma verdadeira descoberta! Yuval Boger, diretor comercial da QuEra, argumentou que, sem a destilação de estados mágicos, os computadores quânticos não têm chance de cumprir seu propósito (que obviamente significa alcançar…).redução exponencial no tempo computacional), e muitas pessoas concordam com isso.

Um exemplo de desdobramento de um arranjo de estabilizadores do tipo X para correção de erros quânticos usando um código Reed-Muller em uma matriz bidimensional. As conexões entre nós adjacentes são fornecidas por quatro qubits adicionais, bem como estabilizadores com peso 2 (d2). O código de repetição, que conterá o estado mágico de saída (sombreamento verde), é combinado com o desdobramento por meio de um procedimento de medição conjunta (sombreamento laranja) (fonte: arxiv.org/abs/2507.12511).
Embora não tenha passado muito tempo desde a publicação da conquista do QuEra na Nature, a destilação de estados mágicos tornou-se um pilar da maioria das novas arquiteturas de computadores quânticos tolerantes a falhas. No entanto, surgiu outro problema: agora é comum que a maior parte dos recursos gastos no desenvolvimento do próximo algoritmo quântico seja destinada à destilação de estados mágicos. Os próprios pioneiros se limitaram a criar cinco qubits auxiliares ruidosos, dos quais, usando o algoritmo de destilação, obtiveram um único portador do estado mágico no nível lógico — demonstrando, assim, pela primeira vez, a possibilidade fundamental de aplicar a destilação a um sistema de Clifford. Quase simultaneamente, os desenvolvedores da Quantinuum relataram a formação bem-sucedida — também usando a destilação de estados mágicos — de uma porta T lógica (a mesma rotação de 45° na esfera de Bloch), que superou qualquer porta T física conhecida até então em termos de precisão operacional. Alice e Bob, os desenvolvedores dos qubits de gato que nossos leitores já conhecem, implementaram um circuito estrutural completo para destilar estados mágicos. Como resultado,Em um computador quântico, onde apenas 53 qubits físicos foram usados para gerar essa “mágica”, eles conseguiram atingir uma precisão computacional de 10⁻⁶ — o que, sem esse esquema, teria exigido cerca de quinhentos qubits físicos. E isso, aparentemente, é apenas o começo: a destilação de estados mágicos promete dar nova vida, pelo menos, aos computadores quânticos baseados em objetos quânticos naturais (átomos neutros, íons, etc.), enquanto sistemas baseados em hardware macroscópico, como transmons, não podem explorar essa brecha para aumentar seu desempenho — pelo menos por enquanto. Quem sabe, talvez eles aprendam a acoplar o mágico coprocessador-destilador quântico com qubits de natureza física completamente diferente? Então o progresso da computação quântica aceleraria de forma verdadeiramente incrível!
pelo menos