Aquele que repete o antigo e aprende o novo pode ser um líder.
Neste artigo, vamos orientá-lo na regressão linear, o algoritmo básico que dá início a qualquer curso de aprendizado de máquina e ciência de dados. Não é fácil escrever sobre um método tão popular sem pular direto para a linguagem das fórmulas. Além disso, por incrível que pareça, mais informações disponíveis nem sempre levam a um melhor entendimento. A maneira mais eficaz, é claro, é dominar a teoria em projetos reais, e aqui tentaremos dizer o máximo possível sobre o que é regressão linear e qual é seu valor excepcional. O material é estruturado de forma que você mesmo decida o quão profundo deseja mergulhar no assunto. Porém, este artigo não será suficiente para você implementar o algoritmo do zero, seu principal objetivo é a sua compreensão intuitiva e, claro, seu interesse pelos problemas de IA.
⇡#Regressão linear: capa do golpe imortal
Em primeiro lugar, você precisa entender que a regressão linear foi desenvolvida no século 19 no campo da estatística para entender a relação entre dados de entrada e saída. A explicabilidade é um dos principais valores, pode-se dizer, o Santo Graal do aprendizado de máquina, pelo qual os pesquisadores de IA (a IA muito explicável) tanto se esforçam. É a explicabilidade que nos permite fazer a previsão mais precisa, que é a principal preocupação da modelagem preditiva, e esse objetivo é atendido pela minimização onipresente do erro do modelo. Onde quer que a modelagem de dados preditiva não seja usada: em negócios e finanças, é claro, marketing e vendas, retenção de clientes, negociação algorítmica; na ciência – em quase todas as áreas. Se ao menos houvesse uma quantidade suficiente de dados numéricos, mas agora não faltam.
BTW, você sabe a diferença entre aprendizado de máquina e modelagem preditiva? Por favor, escreva nos comentários! A resposta estará no próximo artigo do ciclo. Agora, sugerimos que você mergulhe mais fundo no tópico da regressão linear (as associações com o mergulho assombram o autor deste artigo por um motivo desconhecido).
⇡#Preparando-se para um mergulho: verificando seu equipamento
Em primeiro lugar, vamos ter certeza de que você está familiarizado com os conceitos que não pode prescindir.
No contexto do aprendizado de máquina, a regressão linear se refere à seção de aprendizado supervisionado, ou seja, quando a conexão entre a entrada e a saída é claramente traçada e um determinado valor é previsto a partir de um número limitado de exemplos (nos quais, como aluno, o algoritmo é treinado). Lembre-se de que a aprendizagem supervisionada, ou aprendizagem supervisionada, é dividida em duas categorias: regressão e classificação (sobre isso nos materiais a seguir).
Para o aprendizado supervisionado, dividimos os dados em um conjunto de treinamento e um conjunto de teste: 80/20 é a proporção usual. O conjunto de treinamento são os dados com os quais o algoritmo aprenderá. Por exemplo, ao usar regressão linear, os pontos no conjunto de treinamento são usados para construir uma linha de melhor ajuste. O conjunto de teste será usado para avaliar a qualidade do modelo.
Com base nos dados de treinamento, podemos construir um gráfico (por exemplo, o número de horas de aulas de um aluno nele será indicado por x, e sua pontuação final será y) e determinar uma função que será muito semelhante a esta gráfico. Esta função é chamada de função de hipótese, no nosso caso será uma regressão linear unidimensional (com uma variável). Agora, com base na função de hipótese, você pode fazer uma previsão.
A precisão da função de hipótese pode ser medida usando uma função de custo ou uma função de perda. Por que isso é chamado assim? Porque caracteriza a perda de má tomada de decisão com base em dados observáveis. A função de perda leva a diferença entre a função de hipótese nos valores xe o treinamento definido nos mesmos valores x. Nós nos esforçamos para encontrar os parâmetros da função de perda de forma que sua saída seja mínima.
Treinar o modelo é exatamente a minimização da função de perda, e para isso você precisa mover na direção negativa da derivada. Dessa forma, podemos encontrar uma função de hipótese que descreve com mais precisão nossos dados de treinamento. Vamos supor que seja uma regressão linear unidimensional (simples).
⇡#O que é?
A regressão linear é um modelo de dependência linear de uma variável (dependente) de outra ou mais.
A representação matemática da regressão linear é fácil de entender. A linha de regressão linear simples é dada por uma equação da forma y = β0 + β1x, onde x é a variável independente, y é a variável dependente. Como ensinamos na 7ª série!
Regressão linear simples com uma variável explicativa (x): os pontos vermelhos são valores reais, a linha de regressão (y) é a linha de melhor ajuste através dos pontos do gráfico de dispersão
A inclinação da reta neste gráfico é igual ao coeficiente β1, o ponto de interseção (interceptar, interceptar) é definido no coeficiente β0 (ou seja, o que é y em x = 0), este coeficiente dá a nossa liberdade de linha de movimento para cima e para baixo no espaço bidimensional. O algoritmo de aprendizagem busca encontrar esses coeficientes e assim determinar a função de regressão (modelo).
Quando existe uma variável (x) na entrada, esta é uma regressão linear simples; se houver várias delas, já é uma regressão linear múltipla. Um gráfico de regressão linear em duas dimensões (com uma única variável independente) é uma linha reta, em três – um plano, em quatro ou mais – um hiperplano.
Há um enorme potencial por trás dessa simplicidade externa: veremos quantas ideias e oportunidades incríveis surgiram com base neste método com mais de duzentos anos de história. É a regressão linear que fundamenta muitos dos algoritmos mais recentes na vanguarda da ciência, incluindo redes neurais profundas.
⇡#Como funciona?
Como já mencionado, o objetivo do algoritmo de regressão linear é estabelecer tais coeficientes para que seja possível determinar um determinado modelo de regressão, e isso é feito durante o processo de treinamento. Existem vários métodos para fazer isso, mas os mais populares são os mínimos quadrados comuns e a pedra angular do aprendizado de máquina, gradiente descendente.
⇡#Regressão Linear de Mínimos Quadrados Ordinários: Primeiros Passos
Para simplificar, aqui está um exemplo com uma variável independente. Suponha que temos um conjunto de pontos de vista. Pode ser a área dos apartamentos, a altura das pessoas, etc., ou seja, qualquer fator (regressor) cuja influência você queira saber (por exemplo, observe a dependência da altura e do peso, área da habitação e seu custo, etc.). Claro que, na realidade, mais frequentemente de um fator é levado em consideração, mas vários, mas para este caso temos a regressão linear múltipla.
Os dados estão aí, mas agora a questão é: como traçar uma linha reta que ficaria o mais próximo possível desses pontos de observação?
O método dos mínimos quadrados ordinários é projetado para traçar uma linha através da dispersão de pontos de forma que a soma dos quadrados dos desvios dos pontos da linha seja mínima. Em palavras simples: o erro (valor residual, desvio) neste método nada mais é do que a diferença entre “realidade e expectativa”, o valor obtido de y e o valor previsto de ŷ.
E = y – ŷ (valor real – valor previsto).

Geometricamente, é a soma dos comprimentos dos segmentos entre as cruzes vermelhas no gráfico (valores reais) e a linha de regressão, também chamada de linha de tendência.
Os valores ŷ estão na linha de regressão e as cruzes vermelhas representam y. e = y – ŷ (valor real – valor previsto)
A soma dos desvios é quadrada (SSE – soma dos erros quadráticos) e minimizada usando cálculos diferenciais e matriciais, que provavelmente não daremos. Às vezes, não é a soma dos desvios quadrados que é minimizada, mas a média dos erros quadrados (MSE).
Por que exatamente um quadrado? Sempre acreditei que isso é feito para se livrar de valores negativos, mas acontece que o quadrado dos comprimentos dá uma função suave (que tem uma derivada contínua), enquanto simplesmente o comprimento dá uma função em forma de cone que não é diferenciável no ponto mínimo. (No caso de sua curiosidade o levar longe demais.)
O método dos mínimos quadrados, além das vantagens óbvias, também tem uma desvantagem significativa – ele não lida mal com uma grande quantidade de dados de entrada (fatores, ou simplesmente xi). Se você estiver trabalhando com big data, a descida gradiente é sua escolha. Usando esse método, você está fazendo aprendizado de máquina em sua forma clássica, porque é assim que as redes neurais são treinadas, incluindo os algoritmos de aprendizado profundo de última geração que agora estão na vanguarda da ciência.
⇡#Regressão linear com gradiente descendente
⇡#Descida gradiente, mergulho: nível 1
Imagine que você está no topo de uma ravina e quer descer, mas não sabe como. Você caminhará mais largo quando o declive for mais raso e mais raso quando o declive for mais íngreme. Seu próximo passo dependerá do anterior, e quando chegar ao fundo do barranco, você irá parar. Esta imagem ajudará você a entender mais explicações. A inclinação, ou inclinação, de sua ravina (inclinação em seu sentido original, é claro!) Será definida pelo gradiente. Um gradiente, ou inclinação, nada mais é do que a proporção de mudanças no eixo y para mudanças no eixo x.
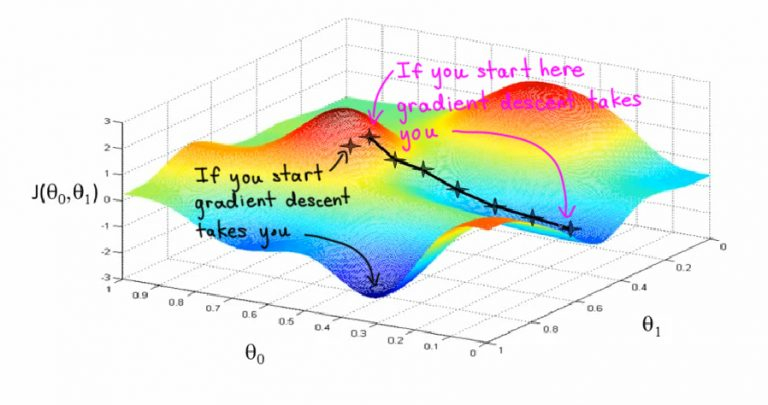
O gradiente descendente é o principal método de treinamento de redes neurais, com a sua ajuda os parâmetros da rede neural (pesos e bias) são gradualmente refinados a fim de minimizar a função de perda de rede (função de custo, função de perda)
⇡#
O objetivo de treinar um algoritmo de aprendizado de máquina é minimizar a função de perda
(Como um lembrete, a função de perda é a diferença entre os valores dos rótulos de treinamento e a previsão feita com o modelo). Como isso acontece?
Se falamos de regressão linear simples (y = β0 + β1 x) em termos de aprendizado de máquina, o intercepto corresponde ao parâmetro β0, e o peso (peso) corresponde ao parâmetro β1. Primeiro, os valores aleatórios são iniciados para cada coeficiente. A soma dos quadrados dos erros é calculada para cada par de valores de entrada e saída. O gradiente de erro será calculado usando as derivadas parciais dos pesos e funções de perda de polarização.
Também precisamos da taxa de aprendizagem, que também é definida empiricamente. Este parâmetro (normalmente denotado como £) determina o tamanho da etapa do gradiente realizada a cada iteração, e é responsável por como os pesos serão ajustados levando em consideração a função de perda. Quanto mais baixo for o valor da taxa de aprendizagem, mais lento será o movimento ao longo do gradiente. Com uma taxa de aprendizado baixa, provavelmente não perderemos um único vale (mínimo local), embora corramos o risco de ficar presos em um platô e, então, teremos que esperar pela convergência.
O processo é repetido até que a soma mínima dos erros quadráticos seja alcançada ou até que nenhuma melhoria adicional seja possível.
⇡#Descida gradiente, mergulho: nível 2
O gradiente descendente é um método iterativo de encontrar o mínimo local de uma função movendo-se ao longo de um gradiente.
Vamos usar a descida gradiente para treinar a regressão linear simples. A função de hipótese será então a função linear
É necessário definir parâmetros Nossa função de hipótese com uma função de custo definida assim:
Dividimos nossos exemplos do conjunto de treinamento por m, observe que os dois no denominador são um truque matemático que usamos para compensar 2 ao tirar a derivada da função. Entre parênteses, a diferença entre os valores reais e as previsões, então tudo é somado e elevado ao quadrado.
Agora precisamos minimizar a função em relação aos seus parâmetros:
Para a regressão linear simples, esses parâmetros podem ser definidos como zero e, no caso de regressão múltipla, você precisará defini-los com valores aleatórios. A seleção de parâmetros é realizada iterando nosso conjunto de treinamento. Atualizaremos os parâmetros de acordo com esta fórmula:
Onde α é a taxa de aprendizagem, e – A derivada, ou inclinação, da função de custo, que nos dá quando substituída
A cada iteração, os parâmetros serão atualizados e a função tenderá para o mínimo.
O algoritmo acima é denominado Batch Gradient Descent nas fontes em inglês, uma vez que todo o conjunto de treinamento (batch) é usado em cada iteração. No entanto, existem variações desse algoritmo, como descida gradiente estocástica e descida gradiente em minilote. Você pode ficar tentado a se familiarizar com eles.
Este material foi criado com grande esperança de que o aprendizado de máquina gradualmente seja percebido não como um abstrato e, o que já está lá, um conceito “promovido”, mas como uma disciplina científica interessante.
Outros materiais do ciclo:
- Inteligência Artificial: Um Algoritmo Genético e Suas Aplicações
- Inteligência artificial: algoritmos de pesquisa
- Eu quero estudar inteligência artificial!
- Ramos e áreas de inteligência artificial: uma visão panorâmica
- Inteligência artificial e consciência: jogo de imitação
- Apresentando a Inteligência Artificial
Fontes: